「TPで障害物を避ける」シリーズpart3（最終回）

今回は、障害物に奥行きを与え、Objパーティクルが障害物を避けるためのターゲットポイントの位置を調整しました。

ターゲットポイントの位置はClosest Point等のちょっとした数学、算数を使いながら求めていきます。Closest Pointについては、以前の記事で触れました。

こういった内容で進めていきますが、ノードの組み方を説明していくと時間がかかってしょうがないので考え方だけを記事にしていけたらと思います。

はじめに、完成動画をご覧ください。


完璧です。と言いたい所なのですが、障害物が複雑に複数配置されていると破綻してしまいますorz
今回はそうならないように、障害物を配置していますw


下図が今回調整した大まかな点になります。

前回から障害物を変更し浮き上がった問題を調整するといった感じです。


では、どのようにターゲットポイントの位置を調整していくかを簡単に図にしました。
アプローチは、色々あると思われますがチュートリアル通りに行いました。

このような感じでターゲットポイントを設定しています。

③の式は自身手こずったので取り上げます。
式だけ見ると算数なんですよね。これ見てパッと理解できず算数力のなさにへこみました。
基礎筋トレしていかないと、筋力が全く足りないです。

最後に、今回はノードの構成というより何をやっているのかに焦点を当てていきました。
こういう何をやっているのかがある程度わかるとすんなり進むと思います。

これでようやく、Joe Scarr氏のDVDのSquirlArt CROWD SETUPSをほぼ終えました。
最初このチュートリアルに入ったときに、ノードの構成＆エクスプレレッションをみて絶望的でしたが、時間かけて少しづつ進めるうちに理解できるようになりました。そして、多くを学ぶことができました。
これまでを見るとわかるとおり数学が多く使われています。
ツールはどんどん新しく変化していきますが数学は変わりません。
と、どこかの本に書いてありましたw
なのでこのチュートリアルは数学を学べるという意味で強く、おススメしますw 

もう一つの感想として、このシステムを完璧にしようとすると、キリがないですw
これは、どのシステムにもいえることかもしれませんね。
自身が大きなシステムとかプログラムとか組んだことないからわからないですが見極めも肝心だと思いました。やっていると、どんどんアイデアが浮かぶものです＾＾あーしたい、こーしたいと。

このチュートリアルでも完璧なシステムに達していないと思います。実際、障害物の配置によって破綻してます。

そこで、SquirlArt CROWD SETUPS最後のflowField 2Dの項目があります。
これはスプラインでパーティクルを誘導するといったアーティストよりな方法をとっています。

なので、全てをプロシージャルにするのは気持ちよいのと思いますが、見極めが肝心ということも勉強になりました。




 

TPで2直線の交点を求める

前回に続き、数学ネタです。
前々から紹介している、こちらをTPでやってみるって感じで進めます。
もう、リンク先見たほうが早いと思いますが。。


図①

はじめに、線分AB上の点を求める式です。
前回の式と同じです。


ＴＰ式①--　Ａｐｏｓ+（ｕｎｉｔ（ＡＢ）*length(ＡＰ）)

今回もベクトルAPを求めていきます。
図①を見るとわかるように、ベクトルＡＰは、点Ａから直線ＣＤの最短距離ではありません。
前回は外積で最短距離求めていきました。
今回も、前回とちょっと使い方は異なりますが、外積を使い求めていきます。

図②

ざざっと図にしてみた。
直線ＣＤに対し、直線ＡＣとＡＢの外積を求めると青線、赤線が求まる。
この青線と赤線、二つの比率がベクトルＡＰの大きさとなる。
つまりＴＰ式①のlength(AP)となる。

いつものように後半、内容スカスカ！？
いつか自分で記事見直したときに調整します。
さらば。サササ、、、－－

TPで、任意の座標からもっとも近い線分上の点を求める

ちょっとタイトルが長くなってしまいました（汗）数学での良い言い回しとかありそうですが。。。
英語では、Closest Pointと言うのですかね？
ここで、躓いてたらいかんので画像でどういった事か説明します。

図①

といった感じです。
点Ａ，Ｂ，Ｃのベクトル値は確定してるものとして進めていきます。
今回は点Ｐを求めるにあたって、外積を使い求めていきます。
内積でも、求められますが 外積で求めていきたいと思います。
理由は、外積だと上で求めたものをちょっと応用すれば直線同士の交差点も求められます。
こんな感じです。 すばらしい！
内積だと、これは無理かな～と。すみません、憶測です^^

では、早速やっていきます。※関数とかＴＰ用の表現を使っています。


はじめに、線分AB上の点を求める式です。こちらにも書きましたが復習です。

図②

ＴＰ式①--　Ａｐｏｓ+（ｕｎｉｔ（ＡＢ）*length(ＡＰ）)

ベクトルAとABは、わかっていますので、ベクトルAPの大きさがわかれば、ベクトルＰが求まります。



では、ベクトルAPの大きさを求めていきます。
わかりやすいように、辺d,e,fを割り当ててみました。
ベクトルAPの大きさがfということですね。

図③

ピタゴラスの定理から、fを求めるにはeとdが解ければ求まりますね。


ＴＰ式②--　f = sqrt(d*d-e*e)


これで、ベクトルAPの大きさは求まります。
後はeとdを埋めていくだけです。

dの方はベクトルＡＣの大きさを求めればよいので、求まります。
さてeですが、ここで外積を使います。

ＴＰ式③--　e = length(AB x AC)/length(AB)
※ＴＰ式③のベクトルABの大きさは、1でもなんでも揃っていれば良いらしい。

式の参考↓

こちらの、2Dでのある点から直線までの距離より

全ての値の準備ができたので、TPに組み込んでいきます。
上記の三つのＴＰ式を組み込みました。

さてさて、これの使いどころはいつになるのやら。。
近々公開かな。

「TPで障害物を避ける」シリーズpart2

前回の記事をpart1として、その続きになります。
といっても、自分のミスの修正です。
こそっと直したいところですが記憶に残しておきたかったので記事にしました。

前回は、障害物が一つだけでした。
まず、前回の設定のまま、障害物を増やしてみました。

動画①



いっこうにGoalに向かってくれないようです。。行き場を失っています＾＾
修正が必要です。

動画②

結果、なんとかＧｏａｌに向かわせることができました。

では、前回の設定を見つつ修正点をメモしていきたいと思います。

まず、動画①の問題点として、
Objパーティクル（三角錐モデル）が最初の障害物を避けた後、Goalに向かってくれないという点です。


前回の記事の④-3でObjパーティクルが最初の障害物を避けた後、ゴールに向かう条件が設定されています。GoalToCheckというダイナミクスです。簡単に言うと、Objパーティクルがゴールを視認することができたらGoalに向かうという条件設定になっています。
動画①では、追加した障害物のせいでObjパーティクルはGoalを視認できない事がわかるかと思います。まさに行き先を見失っているという感じですねw
なので、この条件設定は使えません。

次の条件に変更しました。

Guide for Avoidダイナミクスで取得したターゲットポイントに近づくと、再びゴールを目指すという条件設定です。

これで、万事解決というわけにはいきませんでした。
てか、全然駄目です。

んっと、現状、次に新たに発射されるObjパーティクルからターゲットポイントが作られると、最初のObjパーティクルはそのターゲットポイントが一番近いと判断したらそちらに向かってしまうということになっています。

図にしてみた↓↓

どういう設定かというと、
前回の記事の④-2にあるNearest point searchダイナミクスの設定になります。
このダイナミクスセットでは、毎回全てのターゲットポイントを取得して（PPassAB）、一番近いターゲットポイントを取得するように設定されています。
これでは、上図の右のような結果になるので、PPassABによるターゲットポイントの取得は無理なようです。


なので、PPassABは消して以下のように設定しました。

こうすることで、Objパーティクルはターゲットポイント(ExitPos)を取得したときだけの位置又は方向を毎回取得することができます。ここのデータの流れの詳細な説明は省きます。
簡単に説明すると、図の上のダイナミクスセットはターゲットポイントを取得するためのダイナミクスセットで、下がその取得したターゲットポイントに向かう設定です。


大まかですが、これらのような修正をすることで動画②のような事ができるようになりました。
興味があれば、ファイルアップしますので設定を見比べてみてください^^
又、これらはあくまでも、俺流設定なので間違った点はあるかと思われます。
そして、そういった点や別の良い方法などあれば指摘してくれると助かります。
後、基本的な考え方はJoe Scarr氏のDVDを参考にしています。SquirlArt CROWD SETUPSの項目です。てか、修正するにつれ、その設定に近づいているかも＾＾

part1
part2

次回は、Objパーティクルが避けるためのターゲットポイントの位置を見直していきたいと思います。
こっからが、めっちゃ難しくなるところだと思います。
数学好きにはたまらない内容になるかもです^^

「TPで障害物を避ける」を一旦まとめてみた。

ちょいちょい忙しくて、久々更新です。

以前にも、障害物を避ける件については、チョコチョコ記事にしていたのですが、キリいいところまで来たので一旦まとめようと思います。

まず、基本的な考え方はJoe Scarr氏のDVDを参考にしています。SquirlArt CROWD SETUPS の項目ですね。ご覧になった方は、わかると思うのですが、非常に複雑かつエクスプレッションが頻繁に使われ難しいです。

ですが時間をかけて、チュートリアルを進めるうちに、ある程度つかめてきました。
そして、０から自分でセットアップしてみました。 
結果は、本家と比べ、大分オレオレ設定になってしまいました＾＾
注意点として、今回上記のチュートリアルの項目全てを取り入れたわけではありませんが、大枠は捉えることができたのかなと思っています。
残りは次回にでも記事にできたらなと思います。

では、一つ一つメモする感じで説明していきたいと思います。

はじめに動画をご覧ください↓↓



では、順々にやっていきます。

①このシステムの設計書を適当に文字や図で紙に書く。

みなさん、実際やっていますか？＾＾
あまり大きなシステム作ったことないのであれですが、自分は苦手です。
実際手で動かさないとわからないこともあるし。。
とりあえず、形的にやってみましたって感じです。

②①を元にとりあえず必要なデータ、グループをつくってみた。

プログラマっぽく、グローバルデータをメモリノードに入れてみたw
グループは、はじめから画像のように整理されていたわけではない。後から、このように整理した。

③StartPointからGoalPointまで、パーティクルを移動する。

大きくは↓↓の記事を元に動かしています。
----こちら-----


設定画像↓

ちなみに、水色枠の角度を求める方法かなり使えますので抑えておいたほうが吉！

④障害物を避ける

ここからが、個人的には面白いかなと思います。
やっている事としましては、ある条件を元にサンプルとなるパーティクルを発生させて、それに向かってObjは進行方向を変えるというようなことを行っています。
ちょっと、複雑になりそうなので、さらに見出しを分解してみて行きたいと思います。

1、障害物をサーチします

ある距離になると、障害物をサーチする設定です。サーチした情報はメモリに保存しておきます。

2、障害物を避けるための方向を取得するためにTargetPointを作成します。

1で、サーチした情報を元にTargetPointを作成します。
このTargetPointの作成方法は、こちらを元にしています。
リンクの設定では、同心円状にパーティクル（TargetPoint）を配置しています。
今回は、横一列にパーティクル（TargetPoint）を配置しています。
この違いは、前者が左右、上下に障害物を避けれるように設定できるのに対して、 後者は左右だけです。今回は左右だけでとりあえず進めました。

 

注意点！！TargetPointを取得できたら、ObjはグループをObj GoToGoalからObj Avoid Obstractに変更しています。理由は、進むべきターゲットが変更したのでデータを扱いやすくするためです。後に説明しますが、避けるのを達成できたら、もう一度Obj GoToGoalグループに戻るように設定しています。

3、Objの向きを、2のTargetPointに置き換えます。つまり、障害物を避ける設定です。そして、避けたらGoalへと再び向かいます。

肝となるのが上記の画像に記しているように、再びGoalに向かわせる条件をどうするのかということです。

⑤障害物をサーチした情報をリセットする。

 

④-1で、Obj GoToGoalグループがbool(on)になったままですので、リセットします。
これをリセットしないと、 ④-3で避けて再び戻ったObj GoToGoalはbool(on)になったままですので、毎フレGuideパーティクルが作られます。

⑥Objにシェイプと向きを与える 。

終了～。

TPで回転周りを考察してみた~spin~

追記　2013/01/05
この記事は全体的にまとまっていません(汗)
ちゃんと理解できたら、追記＆整理していきたいと思います。
それなのに記事にしてすみません＋＋
詳しい方からのヘルプ待っています。


今回の記事は、AfterburnをTPで制御してる際に、TPの回転とABの回転を同期したいと思い色々調べました。

これまで、調べたのをメモ代わりに記述していきます。

結論から言うと、海外のフォーラムでのやり取りを参考に調べた限り、激ムズです。てか無理？？
ですが、１軸の同期はできました！！
追記 メモ
Spinノードでxyz軸の数値を[1，0，0]などのように１軸を同期することはできる。[0.3,0.5,0.8]などのような各軸が混ざり合った値は駄目。
ABでは、ワールド空間軸からxyzの回転値を取得し回転するのに対して、TPでは軸を任意の軸に設定し、その軸を元にxyz回転させる模様。。


激ムズ部分について確かなことは言えないのですが、TPのSpinノードによる回転はクオータニオンでクルクル回転していて、ABの回転はオイラーでクルクル回転してるようです。ですので、これらを合わせる必要があると思われます。
まず、オイラーとクオータニオンをなんとなく知ってるようじゃ先に進めません。
ですが、クオータニオンからオイラーの変換とか調べてみると撃沈。

こちらで軽く基礎をつかめましたが、まだまだです。
難しいので、一先ずオイラーとクオータニオンは置いておきます。


まず、TPからABに回転を同期しました。動画をご覧ください。


回転は、ＴＰのＳｐｉｎノードを使用しＸ軸を基準に回転させています。
構成を三つに分けてみました。
①大きい矢印が、ＴＰによるパーティクルシェイプです。
②小さい矢印は、ＴＰによる回転と位置の値をParamBlockで矢印モデルのコントローラーのオイラー回転とポジションXYZに割り当てたものです。
③球はABによるものです。
全てばっちり同期してます。
ノードの構成は、下記に添付。


次に、ＴＰのＳｐｉｎノードで基準軸をランダムにしてみました。
ランダムに回転する方法ってこれですよね？？


残念、①が同期していません。
これが、クオータニオンによるがかかわってきてるのかな～と思いました。
つまり、①はクオータニオンで回転してて、②、③はオイラーで回転しているので
これら二つを一致させて回転しないと同期しないということです。



そこで、②の矢印モデルの回転コントローラーをクオータニオンにしてみました。
クオータニオンは方位を表すものなので①のAlignmentを②のクオータニオン値にParamBlockでつなげました。



①と②が同期しました。やはり①はクオータニオンによる回転です。
ってかそれは、常識なのかな。パーティクルの回転はクオータニオンが基本みたいな。
どなたかご教授ください＾＾


さて、ＡＢと回転が同期できるまで、もう一歩。
なのだが、ＡＢの回転コントローラーをクオータニオンに変化させるなんてことはム～リ～。。
それか、ＴＰのパーティクルの回転をオイラーにするかのどちらかです。なおさらム～リ～。。

ということで、目的は果たせませんでした！！

ＣＧ数学の道は、遠すぎる。。


フォーラムで3akさんから教えてもらったSpinのアウトプットデータストリームが特に役に立ったので要チェック！！

こういう難しい問題を、少しでも英語でやりとりできたのは良かった。
英語もがんばるぜ！！

>>benra
Hi Notchmen. I'm very new to TP, but i am familiar with vector math. If my memory serves me well. the Get direction helper should give you the current x y and z vectors of your particle. these are expressed as unit vectors . The dot product of each of these and world x , y ,z vectors will give you the cosine of the angle between each of them. - this angle i think will be your current rotation of each axis away from each world zero unit vectors. To be more clear - dot product between vectors A and B . = A.B = |A| |B| cos theta .
where
theta = the rotation angle.
|A| = magnitude of A = always 1 for unit vectors.

The Particle data helper also has access to the alignment of your particle - but im still too fresh to TP to know how to access that in terms of rotations.



>>3ak
IMO you don't need math to get rotation - wire spin data to vector and you'll get axis of rotation. Wire spin data to scalar and you'll get angular speed in radians per second.

i just don't remember what kind of data suits afterburn. You can export through 2 channels - vector and float or convert to quaternion (but there is no quat data channel in tp).

TPで障害物をかわすテスト01

Joe氏のDVDを参考に、群集の勉強中～。
一応,、円柱を避けています^^ まだ、完全に避け切れていないですが。。。





にしても、時間かかるわ～。
でもまあ、この群集は、かなり数式使っていたり、アイデア満載で勉強になるから大丈夫。
そのアイデアを一つ上げるとすると、パーティクルをある方向に移動させたいときに、パーティクルをサンプルとして方向を得る方法がある。こんな感じ→→
これで、結構パーティクルの動きを制御できると思う。だが、これをプロシージャルに行うには数学が必要になってくると思う。
パーティクルを動かす、こういうアイデア、数式はツールが変わっても生きてくると思うので、くじけづ食らいついていきたい。
目指すは、Boidシステム！！

TPでベクトルから螺旋表現するにはcross pruduct !!

こちらの動画に対して、iGouさんとのtwitterのやり取りで螺旋表現をクロスベクトルでやったらできますね～とか言ってできなかったら駄目なのでやってみた。

とりあえず、現時点のベロシティにcrossベクトルをaddしたらできた。
一点、注意するのが、crossベクトルを計算するために使うベクトルを用意する必要がある。
やり方としてはこちらを元に作成した。
ビームエフェクトとかに使えるかな～。。

Iteratorで同心円状にパーティクルを配置

Iteratorの基本を米岡さんがまとめてくれています！
自分で記事書かないと覚えないので、メモ程度に作成してみました。

又、今回パーティクルの配置に使用したエクスプレッションについてはこちらにちょこっと書いています。

CGの数学メモ

これまで、TPでパーティクル触ってるうちに学んだものを整理、メモしてみた。

当然のごとく間違って解釈している事もあるかと思うので、その時は突っ込みのほうお願いします。
こちらも、手法見つけるたびに更新していきたいと思いまする。
又、ＴＰのエクスプレッションの記事と、ダブルとこもあるが気にしない。


ベクトル

■ベクトルは方向と大きさを持った値

■空間での、あるポイントのワールド位置座標は原点からのベクトルの成分値である

■ベクトルＡの｜A｜の意味は大きさを表す記号。
絶対値は、全てをプラスにするという意味に思われがちだが
本来の意味は「始まりから終わりまでの距離」である。

■ベクトルの足し算、引き算で何ができるか？
基礎はこちらが、すんごくわかりやすいです^^
線分上の点を求めることができる→こちらの「ベクトルの加算を用いて～・・」のところ
ベクトルの加算で、動きを滑らかな軌道にする事ができる。→こちら
ベクトルの減算で、2点のベクトルを求める事ができる。TPで言う、C distanceノードと思えばよい。→こちら

■内積は何ができるのか？

-----------------------------------------------------------------------------------
式

●二つのベクトルのなす角が求まる。
内積の公式、A*B=｜A｜｜B｜cosθより
cosθを求めればよい。
--追記2012/10/11-
角度として、値を求めるならarccosθとする。
cosθ=0.5の場合、arccosθ=60度
------------------

●ベクトルの投影の長さ（大きさ）が求まる。
A*unit(B)=投影の長さ

-----------------------------------------------------------------------------------
条件命題

●二つのベクトルの垂直チェック

A*B=0ならば垂直

●二つのベクトルの角度情報（二つのベクトルのなす角をθとする）

Ａ*Ｂ>0のとき、θ<90度
Ａ*Ｂ<0のとき、θ>90度
-----------------------------------------------------------------------------------


■外積は何ができるのか？
はじめに、ＡｘＢで表されるｘはcrossという。よってクロス積とも言われる。
結果はベクトル値だが、二次元の場合だとスカラー値になる。

●二つのベクトルに対して、垂直なベクトルが求まる
右手の法則により、垂直の向きを割り出す！
ＡｘＢが上向きなら、ＢｘＡは下向きになる。
右手の手首を、ベクトルＡ，Ｂの交点に置き、親指は立てながら人差し指から薬指までベクトルＡの向きに合わせる。んで、4本の指をベクトルＢに曲げたとき親指の指す方向がＡｘＢになる。

●二つのベクトルのなす角が求まる。（内積使ったほうが早いとのことだが、時と場合による）
外積の公式、｜AｘB｜=｜A｜｜B｜sinθより
sinθを求めればよい。

●ベクトル同士の交点を求める
こちらがすばらしい記事になります。


●ベクトルと点の距離を求める
｜AｘＣ｜/｜B｜

ベクトルの合成で弧を描きならターゲットに移動

ターゲットに向かって、弧を描きながら到達する表現をベクトルの合成を使って行いました。
元ネタは、Joe氏のDVDです。 パートとしては、09_SquirlArt_Crowdsの一部分になります。
一気にやりたいところなのですが、一つ一つ噛み砕いていくのに精一杯です。

手抜きになりますが、一応解説。




いい感じに、曲線の軌跡を残していますね。
これは、ベクトルを毎フレーム足しあわすだけで表現できます。
その足しあわすベクトルは、パーティクルのベロシティとターゲットへのベクトルになります。

イメージ↓↓適当すぎてすんません。

緑ベクトル、青ベクトルの割合で弧を調整することができます。
青ベクトルを大きくすれば弧は大きくなります。ベクトルを大きくするには、スカラー値をかけてやるんでしたね。
今回、スカラー値は0～1の値に正規化しています。これは、単に解かりやすくするためです 。最終的にDrectionInputにいくので正規化されます。

大分、説明を省いた部分がありますが、大事なところは、ベクトルの合成による表現です。
上記のように、ベクトルの合成を毎フレーム行うことで、じわじわとターゲットにベクトルが向くので結果、曲線が表せる ということになります。

今後もこういった、数学的な引き出しをどんどん増やしていきたいところです。

TPでジオメトリの最短点の検出

ジオメトリの最短点を検出し、パーティクルを飛ばす方法です。
他には、こちらの2ページ目のような使い方ができるようです。
以前は、サーフェースのpointを得るにはIntersectでray飛ばして、hitポイントを得ることしかできなかったと思うのですが、TP5からはジオメトリのPointDataを取得できるので便利になったかなと思います。

ですが現状、他に「こういう使い方ができる！」って いう一押しが思いつかないです。
ですので、メモ的な感じで紹介します。

簡単な動画を作ってみました。
緑の点が、パーティクルから視たジオメトリの最短点のポイントデータになります 。

TPでLightTrailを作ってみた。

TP TrailSystem the latest version from notchmen on Vimeo.


先々週から、TPでLightTrailSystemを作ってきたのがとりあえず完成しました。
一応完成はしたものの、やはり、TPはカラー周りの設定が弱い印象がします。
なんとか完成した感じで、このシステムではEmitterがStdShape限定になってしまいました。
つまり、EmitterがGeometryShapeになるとお手上げで、EmitterがStdShapeのSphere,Boxに限定されます。※Facingも使えないです。
こういった、何かを表現するためには何かしらの犠牲が必要になってくるのがＴＰでカラー調整をするときの印象です。
ですが今回の目的は、Emitterの形はSphereで問題ないので良しとしました。


こういった問題はあるものの、やはり表現力はKyTrailの上を行くと思うのでKyTrailでできないときはTPで仕込むのも良いかなと思います。
KyTrailのほうが設定は簡単ですが、一回システム組めば、ＴＰのほうが幸せになるでしょう。
又、有料のKyTrail Proのほうを触ったことがないので、もしかしたら完成動画のようなLightTrailを作れるのかもしれないです。

さて、TPの中身のほうを簡単に記述します。
今回、三つのLightTrailのバージョンを作りました。前のバージョンはvimeoにUPしてます。
はじめの二つは、カラー表現はMaterialTimeノード、シェイプはStdShapeのFacingを使用しました。
最新バージョンでは、カラー表現にH TexmapColor、シェイプはStdShapeのSphereを使用しています。
これら二つの大きな違いは、光跡を色変化させるか先端のエミッターを色変化させるかです。後者のほうが現実的？？なので、後者のほうにシステムをシフトしました。
結果、後者のほうがシステムがシンプルになりました。
レンダ時間も縮まりました。重いところで、ＧＩ込みで1フレ30秒くらいです。

後、以前にも述べたと思いますがMaterialTimeの不安定さはTP5になっても変わっていないようです。トラックビュー開いてレンダリングするとクラッシュします。組み方が悪いのかな～。。

さて、次は花火でも作ろうかな。

TPのGeometryHelperメモ

TP5の新機能のヘルパーノードで、GeometryHelperというのが追加されました。

気になっていたので、どんなことができるのかな～と思いつつ探ってみてみました。

新しくpointデータというものが扱えるらしいです。

pointデータに関しては、memlogさんの記事で、触れられていました。

memlogさんの記事のpointデータと違う意味だったらすみません。

その辺もわかっていないです。

自分はまだ、「pointって頂点じゃないの！？」ってレベルですのでpointデータをあれこれ触るのは早いようですw

ですが、 pointデータ扱えるようになったら幸せになれる予感はします＾＾

とりあえず下に、 GeometryHelperのノード簡単にまとめてみました～。

output値をみればジオメトリから何を取得することができるのか大体かわかると思います。

ちょっと、まだ情報不足すぎて何も言えないです。

TIPSメモ

・頂点のベロシティが取得できる

・

・

TPのHFragmenterノードについて

検証しながらのメモですので、間違ってることあるかもしれません。


はじめに、HfragmenterはGeneratorの部類と考えると良いと思います。
Hfragmenterは、ピックしたオブジェクトの要素を要素を管理することができるようです。

マニュアルでは、構造物を作る際におススメと書かれているっぽい。
では、実際にHfragmenterをいじってみる。

①4つの要素からなるティーポットを解体してみる。

図①

これだけでは、何もおこらない。パーティクル化されるわけでもなく解体されるわけでもない。
このノードは、TP_HFragmenterをオブジェクトに割り当てて設定していなければ話にならないらしい。

図②

パーティクルシェイプ化はされたが、まだ解体はされていない。
これは、各要素をグループにアサインすることで解体されるようだ。

図③

画像では、HFragmenterモディファイヤ上でエレメントごとにグループを作成するやり方を示している。名前は、各々でつけている。グループ作成は 図③のように自動で作成してくれているが、各要素を個別に手動で作成もできる。
実質、これでティーポットの解体はできる。わかりにくいのでTP上でパーティクルの色分け（グループ分け）を行っている。注意するのが、グループをモディファイヤ上でアサインしたからといって、TP上でのグループ分けはされていないということ。パーティクルのグループ分けは別に必要である。

これで、各オブジェクトの要素をパーティクルシェイプ化し、解体できた。

②TPcollapseを使用してみる

①では、モデルの要素からグループを自動に生成（名前付けは手動）してくれたのに対して、TPcollapseでは、モデルの階層構造からグループを自動生成してくれる。名前も自動生成。
注意点として、一番親に TPcollapseをかけるようにすること。TPcollapseはUtilityにあります。
図④

まとめると、HFragmenterは、
オブジェクトの要素を解体し、パーティクルシェイプ化する。
そのパーティクルシェイプをTP上でグループ分けすることができる。
各要素をjointでつなげたりもできる。
これといった使いどころがまだ不鮮明なので、解かり次第更新したい。

●メモ
jointを扱う場合、モディファイヤスタックからjointレベルに入り手動で配置するw

●使いにくい点
・所々でCtrl+Zが利かない。
・モディファイヤからグループ登録ができない。
・TP上でグループ登録するときにパラメーターが表示されない場合がある。TPプロパティを再起動すれば大丈夫。
・Group Asignで複数処理ができない。（例えば、一括で要素のmassを変えたい場合など）
・jointをプロシージャルに扱えない

TPのFragmentノードについて

Fragmentノードは、基本、オブジェクトをポリゴン単位で解体してくれるノードであることがわかった。

図①

図①を見ればわかるように、決して、新しいトポロジを作って分割はしてくれない。

※ちなみに厚みがあるのは、 FragmentノードのFragmentShapeパラメーターで設定しているため。元には厚みはない。

よって、ブーリアン分割やボロノイ分割ではなく、ポリゴン解体と思っておいたほうが良い。
だが、最後に例外①として下記に例外を記している。

まず、このノードの使い道を記してみた。

①rayfireなどでオブジェクトを分割する。
②それらを一つにアタッチする。
③そのオブジェクトをTP側にパーティクルシェイプとしてアサインする。
④Fragmentノードを割り当て、ポリゴンを解体する。
⑤各破片がパーティクルシェイプとして扱えるようになる。 


※追記　2013/08/15
fragmentノードを使用して変化がない場合はThresholdをさげる

次に、Fragmentノードの解体するためのパラメーターを見てみる

 図②

ここで、一番最初に述べた例外をみてみる。
パラメーターのCountを指定するときは、現在のポリゴンから新たに三角メッシュを作っている模様である。 なので、ここではオブジェクトを解体というより分割といっていいのかもしれない。

例外①

まとめとして、
Fragmentノードはポリゴンの解体を目的とするノードだということを覚えておくと良い。

追記2012/09/09
設定によっては要素も解体できるように見せることができるので、ポリゴンの解体だけを目的にするのではない。要素を解体するのにも使うと良いだろう。


※追記　2013/08/15
要素を解体するには、countを１にするかsmooth and distanceを１８０にするか。

fragmentノードは、現在の要素からさらにポリゴン面ごとに分割するということを趣旨にしているためか、わかりづらい。。

FumeFXで核爆発を検証してみた②

Fumefx NuclearExplosion v002 from notchmen on Vimeo.

ディテールアップと煙の上昇を抑えようとして、解像度上げて、TempertureBupyancyをちょい下げたら、思わぬ結果になった。

きのこ煙が大きく広がりすぎちゃった。コンテナはみだしてる～。

脳内補間失敗っす！！

TPでパーティクルのサイズやベロシティにバリエーションをつけるときの注意

もしかしたら、すごい基礎的なことかもしれない。

ちょっと、下記の動画のような問題にぶち当たって、どうしようか迷ってしまった。

Sizeオペレータ、Velocityオペレーターのvariationを使う場合は注意が必要かもです。

二つともseedをいじることができないので、動画の①のようになってしまいます。

②でRandomオペレータを使って、問題を回避しています。

もしかすると、こうやるのが当たり前だったのかな？それとも他に方法が？

FumeFXで核爆発を検証してみた

Fumefx NuclearExplosion v001 from notchmen on Vimeo.


メモリを24GBに増量した記念に、スケール感のある爆発を制作してみようということで、ここ一週間ちょいほど、がんばってみた。
仕事では、こういうスケール感のある爆発は、なかなか携われないです。
けど、いつか携わりたいという気持ちもあるので準備はしておきたいですね。

ということで、先週は自宅マシンフル稼働でした。
が、、やはり一台はキツイです。
それは、トライ＆エラーが必然的に減ることが一番ですかね。
特に、こういったスケールでかめなシーンでは減ると思います。
なぜなら、ローレゾで動き作ってもハイレゾにすると、フルイドの動きや広がり方変わりますよね。
これはローレゾとハイレゾの差が開くほど変化もあると思われます。
だから、ある程度までレゾ上げてやらないと確認にいたりません。
そうするとレゾ上げたら、sim時間がかかります。
結果、トライ＆エラーが減るということです。

ちなみにローレゾでwaveletはどう？と思うのですが、フルイドをモクモクするにはwaveletじゃ無理そうです。
この、今回制作した動画の状態でwavelet使っていれば最高の結果になったかもです。残念ながらその分のキャッシュとっていませんでしたorz

トライ＆エラーを、いかに多くするかは、やはり良いマシンをたくさん用意することですかね。超ベテラン（シミュ一発で十分っしょw）がいれば、あまりトライ＆エラーせずに済みますが。
最低限メモリはいっぱい積ませましょう！！心に余裕ができますw

今回は、マシン一台とあってsimの結果は天への祈りと浅はかな知識、経験便りでしたw
TPはそれらについては、ほぼ皆無だから良いですね。自分の知識＝結果となるみたいな感じですし。まあ、何にせよFumeとはまだ長く付き合っていきそうなのでがんばりたいと思います。

PC周りのメモ～メモリ～

メモリの容量の増量するだけで、数時間かかってしまった。
何をしてるんやら。。。しかも、最終的に不良？明日、メモリもって店に投げつけに行ってやろう。

--追記 2012/08/19--

恥ずかしながら、メモリがしっかりささってなかったようです。すみません。

このマザボちょっと特殊？で、壊れるんじゃないかというぐらい力込めなければいけないようです。

カチっというのが片方しかないし、油断もしてしまいます。

あ～なんだかんだ半日かかった。。

けど、店行く前にもう一度試してよかった。。反省。

-------------------

けど、サポートセンターに電話したところ色々勉強になったのでメモする。


てか、毎日のようにPC触っているのに、PCの知識なさ過ぎw

今回はメモリを2つ差し替えることにした。
家のマザボは４つスロットがあるので、そのうちの二つを差し替える。
久々、PCのドアを開ける。埃が。。。。
それは、さておき（ちゃんと綺麗にした）取り替えるメモリを抜く。
マザーボードごと取り外しメモリを抜きたいが、面倒くさいので隙間から手を上手く入れて差し替えたい。
これ皆さんどうやってるんでしょう。。マザーボードやファンはとっているのでしょうか？
PCによると思いますが、PCの中身めっちゃ不親切な構造なのでファンやらとらないと大変>０<
ねじとか回しにくいのとかありますし。。

とりあえず、差し替え完了。
実装メモリ確認すると、増えてない。認識されてない。
なんで～。。
一回、全部抜いてメモリにプライオリティ高い順に差し込む。
ここのプライオリティというのはメモリを読み込む順番。
そして、起動。。
「ピーピーピー」とビープ音が鳴る。初めて聞いた。

--追記 2012/08/19--

 今回は、メモリが一つも認識されなかったときになったみたいだ。 

-------------------
これは、メモリに問題があるらしい→こちら

ちなみに、

PCは起動時にメモリ→CPU→グラボという順に読み込むらしい。

このビープ音の原因はメモリがしっかり挿さってない事が原因だったみたい。一つもメモリが認識されていないということ。
家のマザボはカチッとしても浮いている場合があるので、ガッツリ押し込まないといけない。

んでビープ音はクリアしたと思ったら、今度はモニタがつかなくなってしまった。ガッデム。
サポートに聞いたところ、モニタがつかなくなる原因は色々ある。
以前にもあった、グラフィックドライバの関係やら接触不良やらの他に、メモリが正常に動作しないと、それ以上先に読み込まないので（上記の読み込みの順番）モニタはオレンジランプのままになるということだ。
ビープ音だけがメモリの異常を知らせることではないのか。。

--追記 2012/08/19--

モニタがつかない件は、なにかしらのメモリ異常があり、読み込みがメモリでストップされてるからかなと思う。ビープ音は鳴らずファンは動いている。なんならビープ音なって異常を知らせてほしいわ。

-------------------
ここも、しっかり挿しなおしたらモニタはついた。なんだそれ。。
んで、実装メモリを確認してみると足りない。。一つ8GBメモリが4GBしか認識されてない模様。


ギブアップ。もう、メモリが悪い。
明日、メモリ買ったお店に行って交換をしてもらおう。
この経験をいかして明日はさくっと変えれると良いな～

--追記 2012/08/19--

店に行く前、もう一度チェック。

一個一個挿してどれが認識していないかを試す。

それを絞って、思いっきり力入れてぶっさす！！

正常に認識しました！

-------------------

あ～PC周りのあれこれはメンドクサイ

TPでBT jointを探ってみた

久々の更新だ～。
といっても、テスト動画のアップのみです。
解説は、次回気力があったら記事にしたいと思います。


動画は、Ragdollの関節であろう場所にjointをかまし、シュミレーションさせています。
これ、もっと面白いことできそうですね。表現の幅が広がります＾＾





TP ragdoll test v01 from notchmen on Vimeo.

maxScriptで行列を勉強してみた④

今回は、逆行列を使い、基底をワールドとローカル変換し合って座標を変換していく。
こうすることで、あるオブジェクトのローカル情報を元に座標変換する事ができる。
要は別の基底（基準）を元に調整できる事ができるということである。

3dsmaxでいう下の赤枠を切り替えて調整するときあるけど、ここイメージすると良いかな。

実例1　マトリックスを使い、ボックスのある頂点を、ティーポットのある頂点へ移動する。

1、ボックスとポットを用意する。頂点番号50をターゲットにする。
ボックスの絶対座標はワールド基底からの値で、ローカル座標はローカル基底からの値である。
ボックスのワールド基底をポットのローカル基底に変換するために下記の2つの基底を用意する。
ボックスのワールド基底の変換行列は、transformプロパティでゲットできる。
ポットのローカル基底が必要なので、逆行列で用意しておく。

2、ティーポットのローカル空間でのボックスの頂点50の座標を求める。そのためには、ボックスの基底をティーポットのローカル空間にすればよい。

3、ポットの頂点100のローカル空間座標を求め、ボックスの頂点50へ移動するため移動ベクトルを求める。

4、後は、3で求めたベクトルをmoveメソッドで頂点100に引数として渡してやるだけだ。

実例2　オブジェクトAのローカル空間を元に、オブジェクトBを動かす。

画像のboxのローカル空間を元にSphereを移動します。ここでは、boxのy軸に沿って移動したいと思います。
①変換マトリクスを用意します。
transmatrix [0,5,0]    ----①
これを$Sphere.transform * transmatrix [0,5,0]してもワールド空間でのY軸に沿っての移動になる。

②boxのローカル空間を取得する
inverse $box.transform    ----②
③①の移動変換マトリクスを②を使い変換する
xformmat ①　②
これでboxのローカル空間でのY軸に沿っての移動になる。

nuclearA_test1

初めてvimeoに動画アップしてみた。
画像圧縮で、ディテールがつぶれているのが残念。要検討。
又、VimeoPlusにしないとアップデートに20分くらい待たされるのかな。それも検討。



nuclearA_test1 from notchmen on Vimeo.




今年、corei7-3930k にしたので、とりあえずFumeで限界辺りまで試してみた。
後半につれ、シミュレーション回らなくなったので（落ちはしないが長い）、あきらめた。
もっと、煙のロール具合を見たかったが、これ以上シミュかけるにはメモリ上げないと駄目っぽい。

構成はこんな感じ。

cpu:corei7-3930k
ram:16gb

res:667x667x1067

FumeFx2.1c

こういう、スケール感大きいものの表現てトライ＆エラーができないのが痛いな～
fumeはmayaとかに比べると大分速いとか聞いたけど、やっぱりまだまだ。。
あきらめることが多いし。数年後に期待。

maxスクリプトで頂点を選択

ふと、スクリプトからオブジェクトの頂点を選択したいと思って調べてみた。
実力不足から、ヘルプを上手く活用することができないのもあり、引くに引けず数時間かかってしまった。ちっくしょう。
まだ、maxscriptの構造がボヤっとしているからスムーズに行かないのだろう。

とまあ一応解決したのでメモです。
別にこれ使って、ツール作るとかじゃないです。只、気持ちをスッキリさせたかっただけです。

では、この数時間の経緯を追ってみたいと思います。

はじめに、選択しているオブジェクトの頂点の番号を与えてやれば消せるだろうと考えました。
頂点番号5の頂点を消すと考えて、イメージ的にselectVert $　5 で消せるかなと。
結果、こんなメソッドは定義されてないということでエラーが出ました。
んで、ヘルプを探りました。慣れないのでどう探したら良いのやら。。
とりあえず、vertexやら何やらで検索かけて探しました。こんなんでよいのか不安になりながら。

するとこういったメソッドを発見
↓↓↓↓
deleteVert

これは、オブジェクトの頂点インデックスを指定して削除するメソッドです。

もう後は、deletevertではなくて頂点選択のメソッドを探すだけかなと思いました。上記のselectＶｅｒｔみたいな。

それがない～んです。
あるのは、
getNumVerts 　--オブジェクトの頂点数をゲットするメソッド
getVert 　--オブジェクトの指定した頂点をpoint3（現在の座標での位置）を返すメソッド

等々。。。


ここで、振り出しに戻り、又検索の嵐。。自暴自棄になってます。成長しないな～。
てか検索、日本語引っかからないのが腹立つ。何か意味があるのかしら？？

そこで「メッシュ頂点の選択：」という欄がありました！
絶対これやん！
getVertSelection
#[]
空の配列マーク？が返ってきた。
ヘルプだと、現時点における頂点の選択セットを返しますということらしい。
このメソッドは選択されている頂点番号を返すだけのようだ。

駄目だ。。もうそんなメソッドないのか。。

またも、しつこくヘルプを探る。ちょっとヘルプの見方に慣れてきた。
とりあえず、頂点はコレクションに格納されているからコレクションのタイプを見てみた。

するとVertexSelection値というのがあった。

バーと流し見してみたら,

select --VertexSelection 内の頂点を選択します。

を発見。と、発見してみたはいいもののってなんだ？

ヘルプより----------------------------------------------------------------------


VertexSelection は、シーン メッシュ ノードの一連の頂点を仮想配列として表します。
これを使用すると、インデックスで頂点にアクセスしたり、頂点間を繰り返したり、マップされた関数を頂点に適用したりできます。

「Editable_Mesh」も参照してください。

VertexSelection 配列は動的です。メッシュ ノードの頂点や選択された頂点の変更に伴って内容が変更されます。

VertexSelection 値はマップ可能です。


----------------------------------------------------------------------------------

では、VertexSelectionを作らなきゃselectできないってことで、用意されているコンストラクタで値を作成してみる。

.selectedVerts 　-- メッシュ オブジェクトで現在選択されている頂点です。

.verts -- メッシュ オブジェクトのすべての頂点、読み込み専用です。

この二つが用意されている。
これを使い、作成してみる。

vtx = $.verts
select vtx

できた！！選択したオブジェクトの頂点全部選択できました！！

うわっ、二行とかしょぼ。

頂点番号で指定する場合は

vtx = $.verts
select vtx[#{8}]


コレクションのインデックスで指定する場合は

vtx = $.verts
select vtx[8]


てとこかな。
他にも、いろいろプロパティやら演算子やらあるけど、とりあえずはここまで。

--追記--07/07--
上記の頂点選択スクリプトは何も選択していない状態では効果が見えない。
なので、オブジェクトを一度選択して、さらに頂点レベルに入って選択しなくては効果が見えない。
例
box001モデルの頂点番号6を選択したいとき

select $box001
subobjectlevel = 1
select $.verts[#{6}]

とする。



まとめ。
なんでこんな時間かかったんやろ。。。
ただ、オブジェクトのプロパティを指定してあげてselectメソッド使うだけなのに。。

TPのエクスプレッションメモ

TPのエクスプレッションで値を操作する手法などをメモしていこうと思います。随時更新ってことで{%ピクトハカセhdeco%}

こういうのは、なるべく多く引き出しがあると良いですね。
とりあえず、考えるより引き出しを多くしていきたいです！

後、関数が使えるとこは関数使っています。関数ヘルプ←式の使い方で検索

※スカラー値の変換であれば、Value To Timeノード+Floatノードを使えば、グラフで変換できるので便利！！←詳細は米岡さんのブログに記されています。
今後ノードのパラメータ上でグラフが扱えることに期待。

はじめに、、
ベクトルについて
①ベクトルは方向と大きさのみを持った値
②空間での、あるポイントのワールド位置座標は原点からのベクトル値である


■スカラー演算

●値の範囲を「0～1」に変換。値を正規化する。

---------------------------
Input値
lifespan = 200
age = 0,1,2,・・・・,200
---------------------------
式
age/lifespan
---------------------------
Output値
0,0.1,0.2,・・・・,1
---------------------------

※正規化とは、値を利用しやすくすること。
例えば、範囲が「23～343」のような任意の値を「0～1」の範囲に値を変換し利用しやすくしたりすること。




●値の「0～1」を「1～0」に反転する

---------------------------
Input値
a = 0,0.1,0.2,・・・・,1
---------------------------
式
1-a
---------------------------
Output値
1.0,0.9,0.8,・・・・,0
---------------------------




●任意の数の比率をフロート値で求める
---------------------------
Input値
a = 30
b = 70
---------------------------
式
a/a+b =x
b/a+b =y
---------------------------
Output値
x=0.3
y=0.7
---------------------------



●値の「0～1」を0.5を最大値とし、0.5以上は0に減っていくようにする

---------------------------
Input値
a = 0,0.1,0.2,・・・・,1
---------------------------
式
0.5-(abs(a-0.5)) //absは絶対値
---------------------------
Output値
0,0.1,0.2,・・・,0.5,0.4,0.3,0.2,0.1,0
---------------------------

●三角関数で曲線を表現する

上手く説明できないのでメモです。
sin(a*b)*c+d

a:位相
a=0,1,2,・・・∞

b:周期
c:振幅
d:初期位置


xにcos、yにsinで円を表現することができる。
さらにzに位相（時間など）を加えることにより、上方に向かう螺旋を表現できる。
a,b,c,dにそれぞれ任意の値を入れ、（ｘ、ｙ、ｚ）に上記の式を入れることにより、様々な曲線を表現できる。
もちろんcosでも良い。

パーティクルを動かすというより、パーティクルの配置に使うほうが良いか。。
動かす場合は、Positionオペレータでフレームごとに位置を与えていく感じ。
よってベロシティが簡単にとれないので、パーティクルを動かすには不向き？
ということは、ベクトルで動かすほうが良い？
すみません、すげー基本的なことかもですが混乱気味なのでダラダラと、とりあえずメモしました。

●オブジェクトを地面に転がせる際に回転を同期させる
1軸　degreerad((X_Position)/(Radius*pi))*360

3軸 quaternionを使用

https://vimeo.com/album/2630843/video/80532054


●剰余を使ってエクスプレッションの値を繰り返す
http://sidefx.jp/doc/ref/expression_cookbook.html

■ベクトル演算

●単位ベクトルを求める
---------------------------
Input値
v1(任意の名前) //ベクトル値

---------------------------
式
unit(v1)
---------------------------
Output値
v3(任意の名前) //v1,v2に対する直角のベクトル
---------------------------


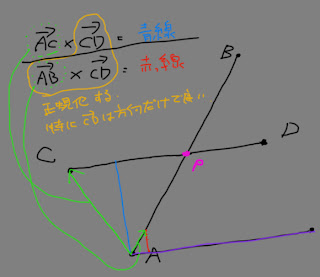
●二つのベクトルに対する直角のベクトルを求める。これを外積という。

---------------------------
Input値
v1(任意の名前) //ベクトル値
v2(任意の名前) //ベクトル値
---------------------------
式
v1xv2
---------------------------
Output値
v3(任意の名前) //v1,v2に対する直角のベクトル
---------------------------

●二つのベクトルのなす角を求める。これを内積という。値はスカラー値になるので注意。


---------------------------
Input値
v1(任意の名前) //ベクトル値
v2(任意の名前) //ベクトル値
---------------------------
式
acos(v1*v2)
---------------------------
Output値
v3(任意の名前) //v1,v2のベクトルのなす角（スカラー値）
---------------------------



●ベクトルの加算を用いて、ある二点（A,B）を結ぶ線上に位置するポイントのワールド位置座標を取得する。

ベクトルを加算する前に、v2の値を決める。
①線分ABの単位ベクトル（方向）を取得する。（TPでいうと、点A,Bをポジションとする、DistanceノードのDirection値）
②ベクトルの大きさを用意する。（スカラー値）
③①と②を乗算することで、大きさと方向を持ったベクトルv2ができあがる。
---------------------------
Input値
v1(任意の名前) //ベクトル値
v2(任意の名前) //ベクトル値
---------------------------
式
v1+v2
---------------------------
Output値
v3(任意の名前) //原点から線分AB上を終点とするベクトル
---------------------------

●ベクトルの減算を用いて、ある二点（A,B）のベクトルを作成する。distanceノードがあるのであまり使い道ないかもだが。。。

●反射ベクトル
Input値
v1(入射ベクトル) //ベクトル値
v2(衝突サーフェスの法線) //ベクトル値
---------------------------
式
(-1*2*(v1*v2)*v2-v1)+v1
(2*(v2*v1)*v1-v2)
---------------------------
Output値
v3(反射ベクトル)
---------------------------



■条件式

if(式,真,偽)
例：if(pos.z>50,1,0)→Zポジが50以上なら、真、以外は偽

TPでパーティクルをサンプルとし障害物を避けてみる。

前回、外積を使用し障害物を避けてみた。
今回は、パーティクルをサンプルし障害物を避けてみる方法をやってみる。
参考は、お馴染みのJoe Scarr氏のDVDより。
このパーティクルをサンプルにする方法は、多方面で応用が利きそうなので要チェック！？

簡単な動画を作ってみた↓↓




ミサイルが赤のパーティクルをサンプルし、障害物を避けている。

詳細は近日。。

パーティクルの衝突の超基礎 #TPJP

先に一言。この記事見たからって、外積が把握できるという内容ではございあせん。
外積の詳細は別のとこでお願いします～

今回記事にしたのは、自身が外積について一つ引っかかったからです。



box（v1）とロケット(v2)の方向を取得し、外積をつかってboxをかわすように、設定してみた。

それがこちら↓↓

v1 x v2





もし、v1、v2が平行ならば、ゼロベクトルになるはず。そうなるよう設定してみた。

だがなっていない↓↓

v1 x v2




デバックで値を確認してみた。




法線のyに意図しない数値はいってる！！ゼロベクトルになっていない！！
もちろん、max上の回転値はall0です！
なのに法線がずれている。。

boxを新しく作り直してみた！！



ゼロベクトルになるとこんな↓↓




では、どのタイミングで意図しない数値が入った？？
一度boxを回転して、回転（0,0,0）と入力で戻すと駄目らしい。0ベクトルには戻れず、何かしら値が入っている。
なぜなら、maxちゃんの0.0って表示は小数点を第何位まで表示すると0になっていない>o<
0.00005213みたいな。。


まあ、結果boxを避けてほしいので0ベクトルにならず良いのだが、気持ち悪い。


んで、気になったのが、このような衝突をセットアップする際、万が一にも0ベクトルになる場合があると思うのですが、それを防ぐ対処法ってあるんですかね？なんとでもなるのかもしれませんが、ベターな方法があれば知りたいものです＾＾

リニアワークフローのリンク集など

■テラオカさん
http://tiraoka.blogspot.jp/2011/10/blog-post.html
■ヤマギシさん
http://yamagishi-2bit.blogspot.jp/2012/05/aecg.html
■イナガキさん
http://ingk-tr.blogspot.jp/2012/04/ae01.html
■Area
http://area.autodesk.jp/column/tutorial/designviz_essence/4_about_linearworkflow_4/
■3DTotal
http://www.3dtotal.com/index_tutorial_detailed.php?id=1531&catDisplay=1&roPos=1&page=1#.T742i8VKT4Q
■seazo
http://www.seazo.no/linear-workflow
■hiroshisaito
http://hiroshisaito.net/blog/2011/05/after-effects-1.html
■CGやり直し
http://mj31000.blog13.fc2.com/blog-entry-76.html
■color is power(合成の式の説明)
http://elephantplus.blogspot.jp/2011/05/nuke-tutorial-over.html

//個人メモ
いつかまとめたい

・vrayの場合、設定でよく見るのがこちらのCバージョンなのだけど、Ａとの違いがわからない。。
違いはＣがレンダリング過程で2.2にしてリニアで返すって事なんだろうけど。。レンダリング過程で2.2にする理由って？？ノイズが出にくいとか？

・普段は整数型（tga,png）で画像処理してたけど、float型（OpenEXRなど）で画像を処理すると、色が破綻するのを防ぎ階調を保てる。環境による費用対効果にもよるけど、どんどん取り入れていきたい。


・３ＤＣＧでレンダリングする場合は,srgbのテクスチャはリニア化して読み込まないと、色が正しく再現されない。

・画像保存時に2.2をかけて保存すると、アンチに影響が出る。

・vrayのレンダリング過程で2.2をかけて1.0で保存すれば、アンチは大丈夫らしい。だけど、リニアのカラー確認ができない。

・ガンマ2.2の環境にする理由。
テクスチャをリニアに変換して読み込みレンダリングするため。
よって正しいテクスチャを元にＧＩも計算されるから、ＧＩもリアルになる。

TPのTimeBaseHelperのリファレンス意訳

TimeBase Helperは、付属のコンディションおよびオペレーターのアニメーションを処理するために、どのタイミングを使用すべきかをコントロールさせます。
ノンリニアアニメーションの背後にある基本的なアイデアのひとつは、
アーティストが固定フレームまたは時間値とは関係なくオブジェクトをアニメーション化することができるということです。
一旦アニメーションが作成されれば、後から全体のアニメーションのスケーリングやモーションのブレンドを調整することができます。
これの良い例は、鳥の群れです。
鳥の翼は、彼らの相対速度によって動きます。
標準的な翼のモーションサイクルが30フレームといいます。
しかし、パニックな鳥をアニメーションさせる必要がある場合はどうしますか？
翼のモーションサイクルは高速になり、多かれ少なかれ移動する必要があります。
低速で移動する群れにも当てはまります 。翼のモーションは遅くなります。
これは完璧な NLA 状況？？（←意味わかりません）
- thinkingParticles とタイムベース ヘルパーを使用して、
自動的にアクションのニーズを満たすためにこの翼移動サイクルのタイミングをスケールすることができます。

TPのTips的メモ

●パーティクルに毎フレーム、ポジションを与えて動かしているときのベロシティのとり方について

O memoryを使用し、前フレームのポジション（depth1）、現在のポジション（depth0）をC distanceノードへ流し、Directionをとってやる。

●O pathfollowはリニアなアニメーションしかできない！？

なので、H Path Positionを使用する。
パスの先端から終端が0-1となるので、時間毎に任意のポジションを与えてやることでカーブアニメーションができる。
問題として、H Path Positionではパスからの距離が取れない。
パスからの距離をとりたい場合は、こちらの⑤より。


●randomにサイズを与えるとき、大きいサイズの割合を多めにしたいとき

TimeToValueを使用し、グラフで割合を決める。

「TPでＩｔｅｒａｔｏｒ,Memory,Psearch周りを探ってみた」のちょっとした概要+α

やりたい表現もなく、TPチュートリアルやって、気になったところ調べてたら、気になったところがどんどん出てきて収集できなくなったパターンです。まあ、なんとか収まりましたが{%トホホwebry%}


とりあえず、その収まった動画です↓





一見、まあなんともない動画ですが学べるものが多くありました。


まず、以前の動画では、核となる黄色の玉が直線的な動きだったので、曲線的な動きにしました。そうした理由はなく、思い付きです{%笑いwebry%}


この、直線的動きを曲線にする手法はこちらから学びました。詳細はそちらをご覧ください。
又、深く（式など）で表現したいならば、こちらのSquirlArt_Crowdsを見るのが良いと思われます。
虫などの群集が障害物を避ける表現ができます！
ですが、今の私には難しく理解不能でした。パーティクル扱うには、やりたい表現なのでいつかリベンジしたいと思います。
よって、今回は前者の手法をとっています。


■では、まず核(nuclear)の動きからです。

--追記0513--
※画像下の入射角と反射角はイコールになる式ではございません。。イコールになるのは入射角が45度の時のみです。この式では入射角が大きいほど反射角は低くなり、入射角が低いほど反射角は大きくなるようです。
正解は米岡さんのこちらのムービーで使用されているようですね。
-------------

上の動画で、球に衝突している部分を、
衝突する前に、コリジョンを曲線的に躱すような表現にしています。

■次に、レーザーの表現についてです

↓↓laser_birthダイナミクスは説明が不十分すぎますね。理由は本人が理解不十分のためです{%トホホwebry%}
補足としてＩｔｅｒａｔｏｒはfor文みたいなもので繰り返し処理をするという認識です。ここでもそうですが、パーティクルの配置などでよく使われることがあるかと思います。

以上です。